Linear Least Square Problem (linear least squares), or ordinary least squares (OLS), is an important computational problem, that arises primarily in applications when it is desired to fit a linear mathematical model to measurements obtained from experiments. The goals of linear least squares are to extract predictions from the measurements and to reduce the effect of measurement errors. Mathematically, it can be stated as the problem of finding an approximate solution to an overdetermined system of linear equations. In statistics, it corresponds to the maximum likelihood estimate for a linear regression with normally distributed error.
Linear least square problems admit a closed-form solution, in contrast to non-linear least squares problems, which often have to be solved by an iterative procedure.
Motivational example
As a result of an experiment, four 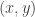 data points were obtained,
data points were obtained,  ,
, 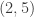 ,
,  , and
, and  (shown in red in the picture on the right). It is desired to find a line
(shown in red in the picture on the right). It is desired to find a line  that fits “best” these four points. In other words, we would like to find the numbers
that fits “best” these four points. In other words, we would like to find the numbers 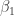 and
and 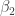 that approximately solve the overdetermined linear system
that approximately solve the overdetermined linear system
 .
.
of four equations in two unknowns in some “best” sense.

The least squares approach to solving this problem is to try to make as small as possible the sum of squares of “errors” between the right- and left-hand sides of these equations, that is, to find the minimum of the function
![\displaystyle S(\beta_1, \beta_2)= \left[6-(\beta_1+1\beta_2)\right]^2 +\left[5-(\beta_1+2\beta_2) \right]^2 +\left[7-(\beta_1 + 3\beta_2)\right]^2 +\left[10-(\beta_1 + 4\beta_2)\right]^2](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+S%28%5Cbeta_1%2C+%5Cbeta_2%29%3D+%5Cleft%5B6-%28%5Cbeta_1%2B1%5Cbeta_2%29%5Cright%5D%5E2+%2B%5Cleft%5B5-%28%5Cbeta_1%2B2%5Cbeta_2%29+%5Cright%5D%5E2+%2B%5Cleft%5B7-%28%5Cbeta_1+%2B+3%5Cbeta_2%29%5Cright%5D%5E2+%2B%5Cleft%5B10-%28%5Cbeta_1+%2B+4%5Cbeta_2%29%5Cright%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) .
.
The minimum is determined by calculating the partial derivatives of  in respect to
in respect to 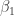 and
and 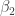 and setting them to zero. This results in a system of two equations in two unknowns, called the normal equations, which, when solved, gives the solution
and setting them to zero. This results in a system of two equations in two unknowns, called the normal equations, which, when solved, gives the solution

and the equation  of the line of best fit. The residuals, that is, the discrepancies between the
of the line of best fit. The residuals, that is, the discrepancies between the  values from the experiment and the
values from the experiment and the  values calculated using the line of best fit are then found to be
values calculated using the line of best fit are then found to be 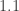 ,
,  ,
,  , and
, and  (see the picture on the right). The minimum value of the sum of squares is
(see the picture on the right). The minimum value of the sum of squares is
 .
.
The general problem
Consider an overdetermined system (there are more equations than unknowns)
 ,
,
of  linear equations in n unknown coefficients,
linear equations in n unknown coefficients, 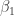 ,
,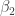 ,…,
,…, , with
, with 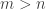 , written in matrix form as
, written in matrix form as  ,where
,where
 .
.
Such a system usually has no solution, and the goal is then to find the coefficients  which fit the equations “best”, in the sense of solving the quadratic minimization problem.
which fit the equations “best”, in the sense of solving the quadratic minimization problem.
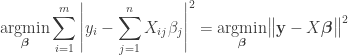 .
.
A justification for choosing this criterion is given in properties below. This minimization problem has a unique solution, provided that the  columns of the matrix
columns of the matrix  are linearly independent, given by solving the normal equations
are linearly independent, given by solving the normal equations
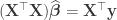 .
.
Singular value decomposition
In linear algebra, the singular value decomposition (SVD) is an important factorization of a rectangular real or complex matrix, with many applications in signal processing and statistics. Applications which employ the SVD include computing the pseudo-inverse, least squares fitting of data, matrix approximation, and determining the rank, range and null space of a matrix.
Suppose  is an
is an  -by-
-by- matrix whose entries come from the field
matrix whose entries come from the field  , which is either the field of real numbers or the field of complex numbers. Then there exists a factorization of the form
, which is either the field of real numbers or the field of complex numbers. Then there exists a factorization of the form
 ,
,
where  is an
is an  -by-
-by- unitary matrix over
unitary matrix over  , the matrix
, the matrix 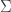 is
is  -by-
-by- diagonal matrix with nonnegative real numbers on the diagonal, and
diagonal matrix with nonnegative real numbers on the diagonal, and  denotes the conjugate transpose of
denotes the conjugate transpose of  , an
, an  -by-
-by- unitary matrix over
unitary matrix over  . Such a factorization is called a singular-value decomposition of
. Such a factorization is called a singular-value decomposition of  . A common convention is to order the diagonal entries
. A common convention is to order the diagonal entries  in non-increasing fashion. In this case, the diagonal matrix
in non-increasing fashion. In this case, the diagonal matrix 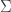 is uniquely determined by
is uniquely determined by  (though the matrices
(though the matrices  and
and  are not). The diagonal entries of
are not). The diagonal entries of 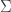 are known as the singular values of
are known as the singular values of  .
.
In practice, matrix  consists of eigenvectors of matrix
consists of eigenvectors of matrix  while matrix
while matrix  consists of eigenvectors of matrix
consists of eigenvectors of matrix 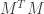 . Finally, matrix
. Finally, matrix 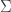 is the square root of a diagonal matrix forming by eigenvalues of either matrix
is the square root of a diagonal matrix forming by eigenvalues of either matrix  or matrix
or matrix 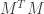 .
.
Example
Let us consider the case when
 .
.
Having  yields
yields

and
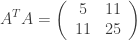 .
.
By simple calculation, one has

being eigenvalues of matrix 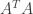 (in the descending form), which helps us to write down
(in the descending form), which helps us to write down

To construct matrix  , one has to find eigenvectors corresponding to eigenvalues
, one has to find eigenvectors corresponding to eigenvalues 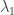 and
and 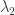 . For the first one, that is,
. For the first one, that is, 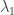 , one has the following linear system
, one has the following linear system

which implies, for example,
 .
.
Similar to 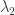 , one has its corresponding eigenvector as follows
, one has its corresponding eigenvector as follows
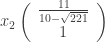 .
.
Thus
 .
.
The numerical solution of  is
is

which gives us
 .
.
Having  we can compute
we can compute  by the following formula
by the following formula 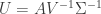 or you can perform the same routine as above. That is
or you can perform the same routine as above. That is
 .
.
It is easy to see that
 .
.
Having a SVD result, that is
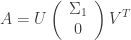
one can see that the solution of 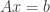 can be computed by
can be computed by
 .
.
Note that matrices  and
and  are not unique. Using Maple software, you can compute SVD as shown below.
are not unique. Using Maple software, you can compute SVD as shown below.

Useful links





 ,
,  with
with  .
.![[a,b]](https://i0.wp.com/alt1.mathlinks.ro/latexrender/pictures/1/4/7/1475c39442659c6febe03b2e1809dbde6ec5fb5a.gif) into
into  subintervals by the following interior points
subintervals by the following interior points  .
.  . T
. T , which will be denoted by
, which will be denoted by  , is called the step size. The value of
, is called the step size. The value of  at step
at step  is usually denoted by
is usually denoted by  , that is,
, that is,  .
.  . T
. T , we can compute the value of
, we can compute the value of  by using the following scheme
by using the following scheme 
 ,
,  , constants.
, constants. th-order system of 1st initial value problems has the form
th-order system of 1st initial value problems has the form 
 ,
,  ,…,
,…, .
.  . We denote by
. We denote by  the following number
the following number 
 , having all
, having all  for all
for all  . To do this, for each
. To do this, for each  ,
,  . More precisely, we need to compute
. More precisely, we need to compute 
 and for each
and for each 
 , with
, with  .
.
 and
and  by using the following scheme
by using the following scheme 
 decomposition (also called a
decomposition (also called a  is a decomposition of
is a decomposition of  where
where  is an orthogonal matrix (meaning that
is an orthogonal matrix (meaning that  ) and
) and  is an upper triangular matrix (also called right triangular matrix). This generalizes to a complex square matrix
is an upper triangular matrix (also called right triangular matrix). This generalizes to a complex square matrix  matrix
matrix  , as the product of an
, as the product of an  unitary matrix
unitary matrix  rows of an
rows of an 
 is an
is an  upper triangular matrix,
upper triangular matrix,  is
is  is
is  , and
, and  the thin
the thin  and we require that the diagonal elements of
and we require that the diagonal elements of  (
( if
if  ,
,  and
and  decompositions
decompositions  being a lower triangular matrix.
being a lower triangular matrix. , one can solve the Least Square Problem
, one can solve the Least Square Problem  where
where  and
and  with
with  . To be precise, by mean of
. To be precise, by mean of ![Q = \left( {\begin{array}{*{20}{c}} {{{\left[ {{Q_1}} \right]}_{m \times n}}} & {{{\left[ {{Q_2}} \right]}_{m \times \...](https://i0.wp.com/alt2.mathlinks.ro/latexrender/pictures/d/1/7/d177fe503a9df3ceca3374824c92382e0a3a61d6.gif)
 . Thus
. Thus  .
.  . Assume that after finishing the Gram–Schmidt process, we obtain
. Assume that after finishing the Gram–Schmidt process, we obtain  . Therefore, we put
. Therefore, we put
 .
.

 , we obtain
, we obtain  from
from  , that is,
, that is, 
 , we firstly project
, we firstly project  onto
onto 







 , one has to find eigenvectors corresponding to eigenvalues
, one has to find eigenvectors corresponding to eigenvalues 


 with the following boundary conditions
with the following boundary conditions







