In this notes, we are particularly interested in some special model of general relativity. More precisely, here we consider the scalar fields since, for example, a real scalar field more or less provides one of the simplest sources of stress-energy in GR.
1. Derivation of stress-energy tensor.
To derive the stress-energy tensor associated to a real scalar field, we make use of the Einstein-Hilbert action. Suppose that the full action of the theory is given by the Einstein–Hilbert term plus a term 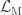 describing any matter fields appearing in the theory, then we have
describing any matter fields appearing in the theory, then we have
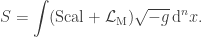
The action principle then tells us that the variation of this action with respect to the inverse metric is zero, yielding 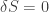 . Calculating this equation gives
. Calculating this equation gives

where the right hand side is nothing but the stress-energy tensor 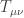 .
.
In modern cosmology, one can introduce on the spacetime  a real scalar field
a real scalar field  with potential
with potential  as a smooth function of
as a smooth function of 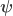 . A particular Einstein field theory is specified by the choice of an action principle with
. A particular Einstein field theory is specified by the choice of an action principle with

To find its associated stress-energy tensor, we first look at  . Since the term
. Since the term 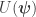 does not depend on the metric, we get
does not depend on the metric, we get

(more…)
in this note
since in our setting
for all
. The quantities
and
come from the Codazzi and Ricci equations. To be precise, we have, by the Codazzi equation,
corresponding to an infinitesimal
variation of the space metric is
is nothing but
. This formula can be applied to
and
to get