This entry can be considered as a continued part to a recent entry where lots of significantly important inequalities (Hardy, Opial, Rellich, Serrin, Caffarelli–Kohn–Nirenberg, Gagliardo-Nirenberg-Sobolev, Horgan) have been considered.
Today we shall continue to list here more important inequalities in the literature. Given 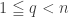 ,
,  ,
, 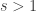 , define the number
, define the number  by
by
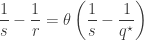
where
 .
.
Gagliardo-Nirenberg’s inequality. For any  one has
one has
 .
.
When 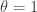 and
and 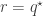 , Gagliardo-Nirenberg’s inequality then becomes the well-known Sobolev inequality.
, Gagliardo-Nirenberg’s inequality then becomes the well-known Sobolev inequality.
Sobolev’s inequality. For any  one has
one has
 .
.
The best constant  has been obtained by Aubin [here] and Talenti [here], independently. Namely, they showed that
has been obtained by Aubin [here] and Talenti [here], independently. Namely, they showed that
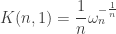
and

where  is the volume of the unit ball in
is the volume of the unit ball in 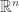 and
and 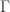 the gamma function.
the gamma function.
When  ,
,  , and
, and  , Gagliardo-Nirenberg’s inequality then becomes the well-known Nash inequality.
, Gagliardo-Nirenberg’s inequality then becomes the well-known Nash inequality.
Nash’s inequality. For any  one has
one has
 .
.
The best constant  for the Nash inequality is given by
for the Nash inequality is given by
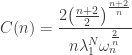
where  is the first non-zero Neumann eigenvalue of the Laplacian operator in the unit ball. This come from a joint work between Carlen and Loss [here].
is the first non-zero Neumann eigenvalue of the Laplacian operator in the unit ball. This come from a joint work between Carlen and Loss [here].
Another consequence of Gagliardo-Nirenberg’s inequality is the logarithmic Sobolev inequality.
logarithmic Sobolev’s inequality. For any  one has
one has

where  also satisfies
also satisfies
 .
.
In fact, it can be obtained as the limit case when 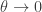 , that is,
, that is,  and
and 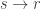 ,
,  . To see this, let us first notice the fact that the constant
. To see this, let us first notice the fact that the constant  in Gagliardo-Nirenberg’s inequality is independent of
in Gagliardo-Nirenberg’s inequality is independent of  . We can rewrite Gagliardo-Nirenberg’s inequality as
. We can rewrite Gagliardo-Nirenberg’s inequality as
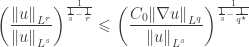
where 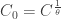 . It then follows that
. It then follows that
 .
.
Thus when  we get
we get
![\displaystyle\int_{{\mathbb{R}^n}} {\left[ {{u^r}\log {{\left( {\frac{u}{{{{\left\| u \right\|}_{{L^r}}}}}} \right)}^r}} \right]dx} \leqq \frac{1}{{\frac{1}{s} - \frac{1}{{{q^ \star }}}}}\left\| u \right\|_{{L^r}}^r\log \left( {{C_0}\frac{{{{\left\| {\nabla u} \right\|}_{{L^q}}}}}{{{{\left\| u \right\|}_{{L^r}}}}}} \right)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cint_%7B%7B%5Cmathbb%7BR%7D%5En%7D%7D+%7B%5Cleft%5B+%7B%7Bu%5Er%7D%5Clog+%7B%7B%5Cleft%28+%7B%5Cfrac%7Bu%7D%7B%7B%7B%7B%5Cleft%5C%7C+u+%5Cright%5C%7C%7D_%7B%7BL%5Er%7D%7D%7D%7D%7D%7D+%5Cright%29%7D%5Er%7D%7D+%5Cright%5Ddx%7D+%5Cleqq+%5Cfrac%7B1%7D%7B%7B%5Cfrac%7B1%7D%7Bs%7D+-+%5Cfrac%7B1%7D%7B%7B%7Bq%5E+%5Cstar+%7D%7D%7D%7D%7D%5Cleft%5C%7C+u+%5Cright%5C%7C_%7B%7BL%5Er%7D%7D%5Er%5Clog+%5Cleft%28+%7B%7BC_0%7D%5Cfrac%7B%7B%7B%7B%5Cleft%5C%7C+%7B%5Cnabla+u%7D+%5Cright%5C%7C%7D_%7B%7BL%5Eq%7D%7D%7D%7D%7D%7B%7B%7B%7B%5Cleft%5C%7C+u+%5Cright%5C%7C%7D_%7B%7BL%5Er%7D%7D%7D%7D%7D%7D+%5Cright%29&bg=ffffff&fg=333333&s=0&c=20201002)
where we have used the fact that the function
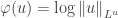
satisfies
![\displaystyle - \left\| u \right\|_{{L^r}}^r\varphi '\left( {\frac{1}{r}} \right) = \int_{{\mathbb{R}^n}} {\left[ {{u^r}\log {{\left( {\frac{u}{{{{\left\| u \right\|}_{{L^r}}}}}} \right)}^r}} \right]dx}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+-+%5Cleft%5C%7C+u+%5Cright%5C%7C_%7B%7BL%5Er%7D%7D%5Er%5Cvarphi+%27%5Cleft%28+%7B%5Cfrac%7B1%7D%7Br%7D%7D+%5Cright%29+%3D+%5Cint_%7B%7B%5Cmathbb%7BR%7D%5En%7D%7D+%7B%5Cleft%5B+%7B%7Bu%5Er%7D%5Clog+%7B%7B%5Cleft%28+%7B%5Cfrac%7Bu%7D%7B%7B%7B%7B%5Cleft%5C%7C+u+%5Cright%5C%7C%7D_%7B%7BL%5Er%7D%7D%7D%7D%7D%7D+%5Cright%29%7D%5Er%7D%7D+%5Cright%5Ddx%7D+&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Therefore, replacing 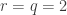 and writing
and writing 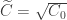 , we obtain the logarithmic Sobolev’s inequality.
, we obtain the logarithmic Sobolev’s inequality.
The best constant for the logarithmic Sobolev inequality is given by
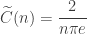 .
.
We refer the reader to a book due to Hebey entitled “Nonlinear analysis on manifolds: Sobolev spaces and inequalities” for details.
The best constant for the Gagliardo-Nirenberg inequality is not completely solved. In some cases, we was able to find its best constants [here, here].
See also: Sobolev type inequalities on Riemannian manifolds
solution to
we denote the integral
. We call
the average of
on the sphere
of radius
, or sphere mean of a function around the origin. In this context, we simply have
.