In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great importance in the modern, direct methods of the calculus of variations. A very closely related result is the Friedrichs’ inequality.
This topic will cover two versions of the Poincaré inequality, one is for  spaces and the other is for
spaces and the other is for  spaces.
spaces.
The classical Poincaré inequality for  spaces. Assume that
spaces. Assume that  and that
and that  is a bounded open subset of the
is a bounded open subset of the  –dimensional Euclidean space
–dimensional Euclidean space 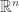 with a Lipschitz boundary (i.e.,
with a Lipschitz boundary (i.e.,  is an open, bounded Lipschitz domain). Then there exists a constant
is an open, bounded Lipschitz domain). Then there exists a constant  , depending only on
, depending only on  and
and  , such that for every function
, such that for every function  in the Sobolev space
in the Sobolev space  ,
,
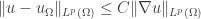 ,
,
where

is the average value of  over
over  , with
, with  standing for the Lebesgue measure of the domain
standing for the Lebesgue measure of the domain  .
.
Proof. We argue by contradiction. Were the stated estimate false, there would exist for each integer 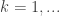 a function
a function 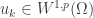 satisfying
satisfying
 .
.
We renormalize by defining
 .
.
Then

and therefore
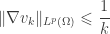 .
.
In particular the functions  are bounded in
are bounded in  .
.
By mean of the Rellich-Kondrachov Theorem, there exists a subsequence  and a function
and a function 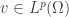 such that
such that
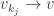 in
in  .
.
Passing to a limit, one easily gets
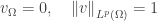 .
.
On the other hand, for each 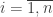 and
and  ,
,
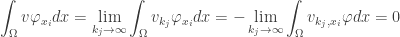 .
.
Consequently,  with
with 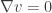 a.e. Thus
a.e. Thus  is constant since
is constant since  is connected. Since
is connected. Since  then
then  . This contradicts to
. This contradicts to  .
.
The Poincaré inequality for  spaces. Assume that
spaces. Assume that  is a bounded open subset of the
is a bounded open subset of the  -dimensional Euclidean space
-dimensional Euclidean space 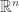 with a Lipschitz boundary (i.e.,
with a Lipschitz boundary (i.e.,  is an open, bounded Lipschitz domain). Then there exists a constant
is an open, bounded Lipschitz domain). Then there exists a constant  , depending only on
, depending only on  such that for every function
such that for every function  in the Sobolev space
in the Sobolev space  ,
,
 .
.
Proof. Assume  can be enclosed in a cube
can be enclosed in a cube
 .
.
Then for any  , we have
, we have
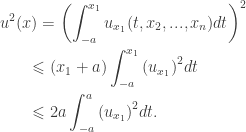 .
.
Thus
 .
.
Integration over  from
from 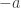 to
to  gives the result.
gives the result.
The Poincaré inequality for  spaces. Assume that
spaces. Assume that  and that
and that  is a bounded open subset of the
is a bounded open subset of the  -dimensional Euclidean space
-dimensional Euclidean space 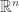 with a Lipschitz boundary (i.e.,
with a Lipschitz boundary (i.e.,  is an open, bounded Lipschitz domain). Then there exists a constant
is an open, bounded Lipschitz domain). Then there exists a constant  , depending only on
, depending only on  and
and  , such that for every function
, such that for every function  in the Sobolev space
in the Sobolev space  ,
,
 ,
,
where  is defined to be
is defined to be  .
.
Proof. The proof of this version is exactly the same to the proof of  case.
case.
Remark. The point  on the boundary of
on the boundary of  is important. Otherwise, the constant function will not satisfy the Poincaré inequality. In order to avoid this restriction, a weight has been added like the classical Poincaré inequality for
is important. Otherwise, the constant function will not satisfy the Poincaré inequality. In order to avoid this restriction, a weight has been added like the classical Poincaré inequality for  case. Sometimes, the Poincaré inequality for
case. Sometimes, the Poincaré inequality for  spaces is called the Sobolev inequality.
spaces is called the Sobolev inequality.
-norm of solution to homogeneous wave equations. Let
be a solution of the Cauchy problem
.
. If
.
such that
.
.
.
,
,
. This is a contradiction provided that
.
. We will show that there exists a non-negative constant
such that
.
denote the Fourier transform of
with respect to the variable
. By taking the Fourier transform of the wave equation and the initial conditions we can get
.
.
.
is positive if
.



 This picture shows the shape of solution in the spacetime.
This picture shows the shape of solution in the spacetime.