In this entry, we shall discuss a geometric meaning of subharmonic functions. This will help us to easily remember the definition of subharmonic functions.
In mathematics, a harmonic function is a twice continuously differentiable function  (where
(where  is an open subset of
is an open subset of 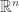 ) which satisfies Laplace’s equation, i.e.
) which satisfies Laplace’s equation, i.e.
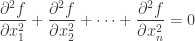
everywhere on  . This is usually written as
. This is usually written as
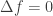 .
.
In 1D, this condition is about to say that  is harmonic if and only if
is harmonic if and only if  is linear. Concerning to the case of functions with one-variable, we have the s0-called convexity saying that function
is linear. Concerning to the case of functions with one-variable, we have the s0-called convexity saying that function  is convex if and only if the function lies below or on the straight line segment connecting two points, for any two points in the interval. Mathematically, a function
is convex if and only if the function lies below or on the straight line segment connecting two points, for any two points in the interval. Mathematically, a function  is said to be convex if
is said to be convex if
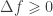 .
.
In higher dimension, the notion of linearity and convexity become harmonicity and subharmonicity. Precisely, two points mentioned above become a hyper-surface, for e.g. like a curve in 2D and a straight line becomes a graph of harmonic function. In practice, the closed interval connecting those two points will be replaced by a closed ball. Therefore, we have
Definition. A  function that satisfies
function that satisfies  is called subharmonic. More generally, a function is subharmonic if and only if, in the interior of any ball in its domain, its graph lies below that of the harmonic function interpolating its boundary values on the ball.
is called subharmonic. More generally, a function is subharmonic if and only if, in the interior of any ball in its domain, its graph lies below that of the harmonic function interpolating its boundary values on the ball.
Let us consider several examples in 2D.
 functions.
functions.
It is well-known that in 2D function 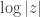 , where
, where  , is harmonic. Therefore, every functions lying below the graph of
, is harmonic. Therefore, every functions lying below the graph of 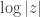 turns out to be subharmonic.
turns out to be subharmonic.
 functions.
functions.
Again, one can easily show that  is harmonic.
is harmonic.
be a bounded analytic function in the strip
. Denote
.
. By the hypothesis, the function
is in absolute value
for
and
. So, by the maximum principle applied in the strip
,
;
, the inequality follows.
