In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great importance in the modern, direct methods of the calculus of variations. A very closely related result is the Friedrichs’ inequality.
This topic will cover two versions of the Poincaré inequality, one is for spaces and the other is for
spaces.
The classical Poincaré inequality for spaces. Assume that
and that
is a bounded open subset of the
–dimensional Euclidean space
with a Lipschitz boundary (i.e.,
is an open, bounded Lipschitz domain). Then there exists a constant
, depending only on
and
, such that for every function
in the Sobolev space
,
,
where
is the average value of over
, with
standing for the Lebesgue measure of the domain
.
Proof. We argue by contradiction. Were the stated estimate false, there would exist for each integer a function
satisfying
.
We renormalize by defining
.
Then
and therefore
.
In particular the functions are bounded in
.
By mean of the Rellich-Kondrachov Theorem, there exists a subsequence and a function
such that
in
.
Passing to a limit, one easily gets
.
On the other hand, for each and
,
.
Consequently, with
a.e. Thus
is constant since
is connected. Since
then
. This contradicts to
.
The Poincaré inequality for spaces. Assume that
is a bounded open subset of the
-dimensional Euclidean space
with a Lipschitz boundary (i.e.,
is an open, bounded Lipschitz domain). Then there exists a constant
, depending only on
such that for every function
in the Sobolev space
,
.
Proof. Assume can be enclosed in a cube
.
Then for any , we have
.
Thus
.
Integration over from
to
gives the result.
The Poincaré inequality for spaces. Assume that
and that
is a bounded open subset of the
-dimensional Euclidean space
with a Lipschitz boundary (i.e.,
is an open, bounded Lipschitz domain). Then there exists a constant
, depending only on
and
, such that for every function
in the Sobolev space
,
,
where is defined to be
.
Proof. The proof of this version is exactly the same to the proof of case.
Remark. The point on the boundary of
is important. Otherwise, the constant function will not satisfy the Poincaré inequality. In order to avoid this restriction, a weight has been added like the classical Poincaré inequality for
case. Sometimes, the Poincaré inequality for
spaces is called the Sobolev inequality.
Hi, is there any book where I can get the proof (or alternative proof) of ?
?
Comment by Daniel — May 2, 2011 @ 11:17
You can read it from Evans’s book, page 263.
Comment by Ngô Quốc Anh — May 2, 2011 @ 12:21
Hi, why can you apply in the first proof the Rellich-Kondrachov theorem? As stated in Wikipedia, this requires that p is smaller than n.
Comment by Marc — July 4, 2011 @ 3:14
Thanks Marc for the question. In view of the Morrey theorem, if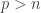 , you can embed
, you can embed  into some Holder space. Thanks to Arzela-Ascoli theorem, you may prove the desired result. For the critical case,
into some Holder space. Thanks to Arzela-Ascoli theorem, you may prove the desired result. For the critical case,  , note that
, note that  as
as  from the left.
from the left.
Comment by Ngô Quốc Anh — July 4, 2011 @ 13:59
Hi again, I found the general version of the Rellich-Kondrachov theorem, from which indeed it follows that the embedding W^1,p —> L^p is compact, for all p=1. I still wanted to ask if you have a proof of the fact, that for n>=2 (I know the proof of the case n=1), if the domain is connected, then if v in W^1,p satisfies grad v = 0 distributionally (!!!), it follows that v is constant (a.e.). Thanks!
Comment by Marc — July 4, 2011 @ 4:14
You may read the proof of Corollary 2.1.9 from a book entitled “Weakly Differentiable Functions” by Ziemer.
Comment by Ngô Quốc Anh — July 5, 2011 @ 1:21
Hi , Why is it that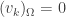 in the proof of classical inequality. Can you give me a explanation. 🙂 Nice work.
in the proof of classical inequality. Can you give me a explanation. 🙂 Nice work.
Comment by Ananda — June 15, 2012 @ 22:42
Hi, my guess is the following: from the choice of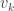 , by taking the average, it is automatically zero (just look at the formula for
, by taking the average, it is automatically zero (just look at the formula for 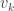 in terms of
in terms of 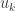 ).
).
Comment by Ngô Quốc Anh — June 15, 2012 @ 23:28
Hi! How does the constant in the inequality for
in the inequality for  depend on explicitly on the domain? And is there any result about the relationship between
depend on explicitly on the domain? And is there any result about the relationship between 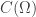 and
and  for e.g.
for e.g.  ? Thanks for your answer!
? Thanks for your answer!
Comment by Paul — May 9, 2013 @ 17:46
Hi, thanks for your interest in my blog. Concerning to your question, the constant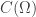 is known as the best constant in the literature.
is known as the best constant in the literature.
It is really hard to find any precise formula the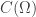 appearing in the Poincaré inequality. Loosely speaking, an estimate like lower or upper bounds for
appearing in the Poincaré inequality. Loosely speaking, an estimate like lower or upper bounds for 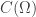 could be a very good and deep result, surely worth publication.
could be a very good and deep result, surely worth publication.
As you may know, the best constant for the Sobolev inequality took a very long time and by many great mathematicians to figure it out such as Thierry Aubin and Giorgio Talenti. For the Poincare inequality, we can find the best constant for some special domains such as convex domains.
Comment by Ngô Quốc Anh — May 10, 2013 @ 6:44
Hi, about the inequality for , what happens when the domain
, what happens when the domain  is unbounded? Thanks for your answer!
is unbounded? Thanks for your answer!
Comment by Dang Son — November 16, 2013 @ 18:57
Thank Dang Son for raising the question.
At the moment, I am not so sure about the answer but I guess it cannot be true. Well, for the case of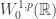 , it is pretty easy to construct counter-examples by enlarging the support of the standard bubble functions. This could work in
, it is pretty easy to construct counter-examples by enlarging the support of the standard bubble functions. This could work in 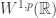 but I have not calculated yet.
but I have not calculated yet.
Comment by Ngô Quốc Anh — November 17, 2013 @ 23:26
Hi! Thank you for useful information. I have a question. Why this limit is equal to zero?
Comment by Liza — November 27, 2013 @ 3:19
Dear Liza,
Thanks for your interest in my post. The answer for your question is as follows:
Since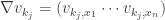 , you can estimate using the Holder inequality as follows
, you can estimate using the Holder inequality as follows
Comment by Ngô Quốc Anh — November 27, 2013 @ 3:55
Hi! I want to say thank you, i get more useful information here. And today I have a question about the Poincare inequality.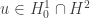 , so the inequality below is true:
, so the inequality below is true:
Suppose that
Thanks for your answer!
Comment by Dang Son — February 19, 2014 @ 22:15
Hi, thanks for your interest in my blog. Regarding to your question, it should be true. The point is that on the Sobolev space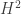 , the usual norm is given as the following
, the usual norm is given as the following
Having the fact that the trace of vanishes on the boundary, the leading term
vanishes on the boundary, the leading term  should dominate the lower order term
should dominate the lower order term  , up to some multiplicative constant.
, up to some multiplicative constant.
I hope this is clear for you.
Comment by Ngô Quốc Anh — February 19, 2014 @ 22:22
Around Poincare inequality, it is interesting. And i have seen an inequality in some paper. It’s like this
where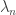 is the eigenvalue of Laplace operator.
is the eigenvalue of Laplace operator.
How about your thinking?
Comment by Dang Son — April 11, 2014 @ 9:34
Hi Dang Son,
Again, thanks for raising the question.
Technically, there is no way (or impossible) to control terms of higher order derivatives in terms of terms of lower ones, such as those you said. However, and I am not sure if you are aware of, one can have some kind of inverse Poincare inequality. When I took a course named Finite Element Method when I was in graduate school, I realized that the following holds
for any quasi-uniform mesh.
Comment by Ngô Quốc Anh — April 11, 2014 @ 12:26
Hi, there is a book where i can get the proof of poincaré inequality on the unit cube? [0,1]^n
Comment by dan — November 15, 2015 @ 22:54
Hi, I do not know a particular book at the moment, I just googled and found this
Boundary Value Problems and Fourier Expansions by Charles R. MacCluer
Let me know if you are not satisfied with this.
Comment by Ngô Quốc Anh — November 15, 2015 @ 23:07
[…] am reading POincare inequality from Evans ( can be found here : https://anhngq.wordpress.com/2010/02/22/the-poincare-inequality/ ) and i am having some trouble understanding it . I would be glad if someone could explain the […]
Pingback by Some questions on the proof of Poincare inequality. - MathHub — April 4, 2016 @ 7:03
[…] found the answer at https://anhngq.wordpress.com/2010/02/22/the-poincare-inequality/. By Holder’s Inequality and Poincare’s Inequality for W1,p0 spaces, there exist […]
Pingback by Poincare inequality? – Math Solution — March 29, 2022 @ 11:39