Today, let us discuss a very interesting stuff. Let say  is a compact manifold without boundary of dimention
is a compact manifold without boundary of dimention 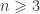 .
.
On  , we consider the following simple PDE
, we consider the following simple PDE

where 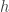 and
and  are smooth functions with
are smooth functions with 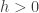 and
and 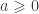 . Since
. Since 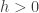 , it is well-known that the operator
, it is well-known that the operator 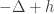 is coercive, see here. A standard variation method tells us that there exists a weak solution
is coercive, see here. A standard variation method tells us that there exists a weak solution  to the above PDE. By regularity theorem,
to the above PDE. By regularity theorem,  is at least a
is at least a  function, thus, a strong solution (in the classical sense).
function, thus, a strong solution (in the classical sense).
Next, we claim that  . To this purpose, assume that the solution
. To this purpose, assume that the solution  achieves its minimum at some point
achieves its minimum at some point 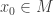 . In particular, there holds
. In particular, there holds
 .
.
This, together with the fact that 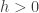 and
and 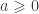 , implies that
, implies that 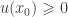 . Thus, we have shown that
. Thus, we have shown that  in
in  .
.
Once we have the non-negativity of  , in view of the strong maximum principle, either
, in view of the strong maximum principle, either  in
in  or
or  . In other words, the solution
. In other words, the solution  cannot achieves its minimum inside the manifold. Since the manifold has no boundary, it is natural to think that the solution
cannot achieves its minimum inside the manifold. Since the manifold has no boundary, it is natural to think that the solution  cannot achieve its minimum although
cannot achieve its minimum although  . This is clear a contradiction to the fact that the manifold is compact and
. This is clear a contradiction to the fact that the manifold is compact and  is of class
is of class  .
.
So something went wrong but what and why?
In fact, we have made a small mistake. In view of the strong maximum principle, we can only claim that the solution can only achieve its non-positive minimum value on the boundary. Therefore, there are cases so that  may achieve its positive minimum inside
may achieve its positive minimum inside  . Thus, there is no contradiction here.
. Thus, there is no contradiction here.
In order to see this, let us go back to a proof of the strong maximum principle. Roughly speaking, it starts with the following simple one.
Lemma 1. If  at any point in
at any point in  , then
, then  cannot have non-positive minimum value in
cannot have non-positive minimum value in  .
.
Proof. The proof is standard. Assume that at 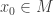 , the function
, the function  realizes its minimum, besides,
realizes its minimum, besides,  . In particular,
. In particular,  and
and 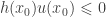 . These force
. These force  at
at 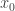 . A contradiction.
. A contradiction.
Form the proof above, if 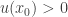 , we cannot get any contradiction. This is why we can claim either
, we cannot get any contradiction. This is why we can claim either  or
or  since
since  can achieve its positive minimum in
can achieve its positive minimum in  .
.
Notice that, if we don’t have any 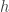 (in the operator), the non-positivity can be dropped.
(in the operator), the non-positivity can be dropped.
of dimension
, it can be stated as follows
be a compact Riemannian manifold of dimension
. Let
be such that
where
is a function such that
is monotone increasing w.r.t the variable
) and that
and for some constant
. If
in
and
does not vanish identically, then
in
.